非負行列

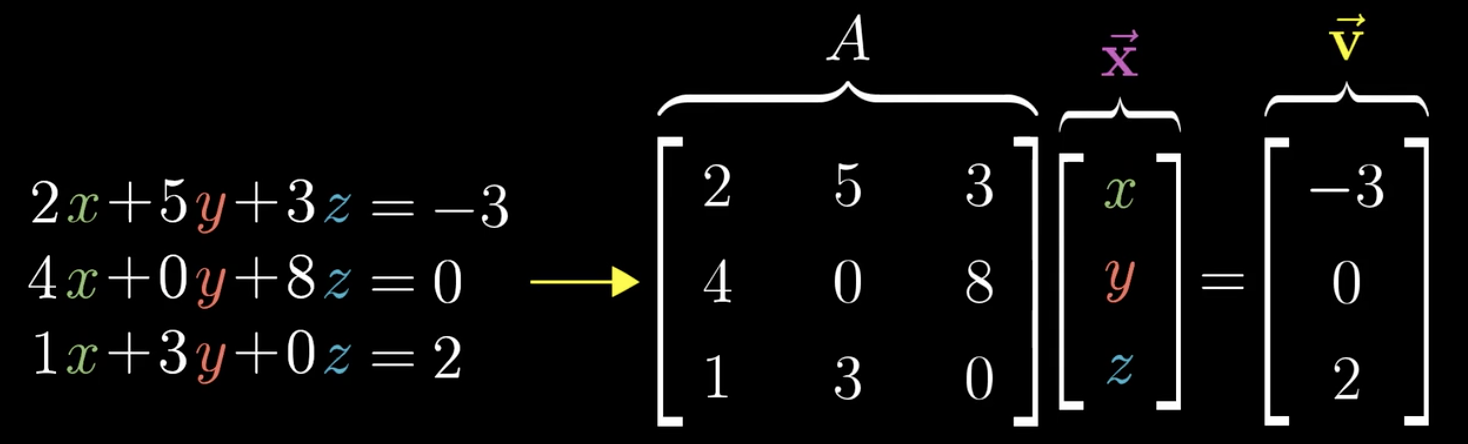
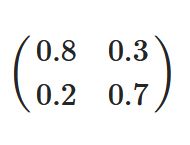数学の分野において、非負行列（ひふぎょうれつ、英: nonnegative matrix）とは、すべての成分がゼロ以上であるような行列、すなわち

${\displaystyle \mathbf {X} \geq 0,\qquad \forall i,j\,x_{ij}\geq 0}$

であるような行列の X のことを言う。正行列（せいぎょうれつ、positive matrix）とは、すべての成分がゼロよりも厳密に大きい行列のことを言う。正行列の集合は、すべての非負行列の集合の部分集合である。

マルコフ連鎖に関する遷移行列は、非負行列である。

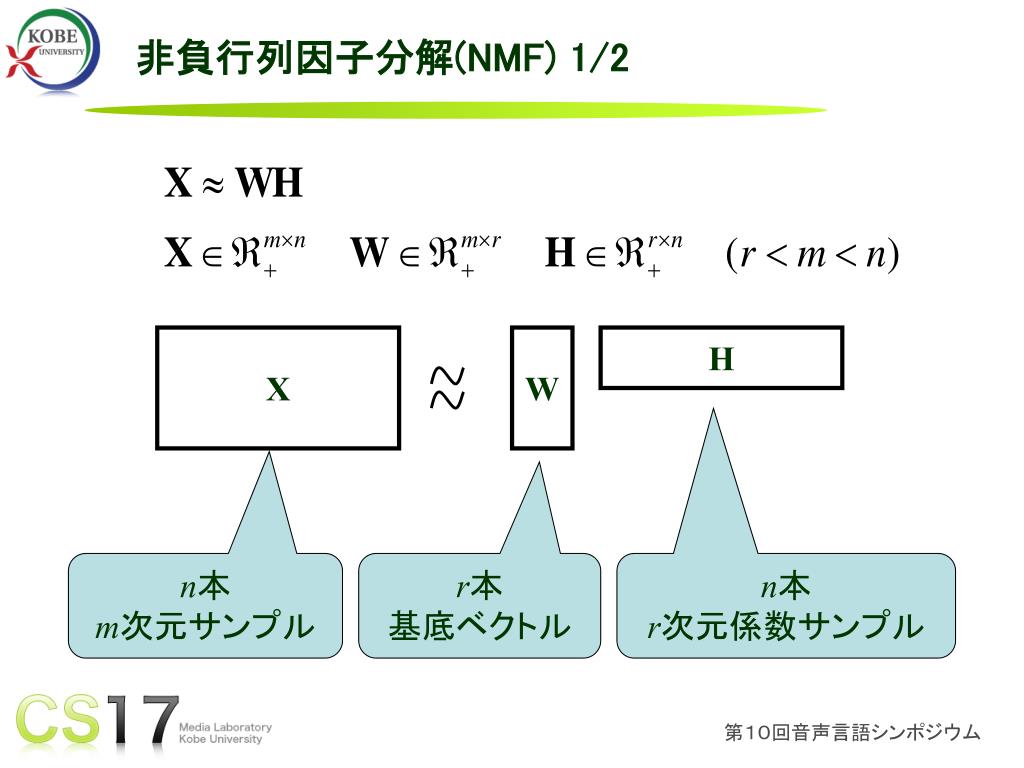
長方形非負行列は、非負行列因子分解を介した二つの異なる非負行列の分解によって近似することが出来る。

正行列は、正定値行列とは異なる。非負かつ正半定値であるような行列は、二重非負行列（doubly non-negative matrix）と呼ばれる。

正の正方行列の固有値と固有ベクトルは、ペロン＝フロベニウスの定理によって表現される。

逆行列

任意の非特異M-行列の逆行列は、非負行列である。もしその非特異M-行列がさらに対称行列でもあるなら、それはスティルチェス行列と呼ばれる。

非負行列の逆行列は、通常は非負行列ではない。その例外として、非負の単項行列が挙げられる。すなわち、非負行列の逆行列がふたたび非負行列であるための必要十分条件は、それが（非負の）単項行列であることである。したがって、正行列は次元 ${\displaystyle n>1}$ に対して単項行列でないことに注意すれば、そのような正行列の逆行列は、正行列でも非負行列ですらも無いという事実に注意されたい。

特殊化

特殊化された非負行列には多くのグループが存在する。例えば、確率行列、二重確率行列、対称非負行列などが挙げられる。

関連項目

• メッツラー行列
• 非負値行列因子分解

参考文献

1. Abraham Berman, Robert J. Plemmons, Nonnegative Matrices in the Mathematical Sciences, 1994, SIAM. ISBN 0-89871-321-8.
2. A. Berman and R. J. Plemmons, Nonnegative Matrices in the Mathematical Sciences, Academic Press, 1979 (chapter 2), ISBN 0-12-092250-9 ※これが初版で、1994年のSIAMのものはこれの再発行。
3. R. A. Horn and C. R. Johnson, Matrix Analysis, Cambridge University Press, 1990 (chapter 8).
4. Krasnosel'skii, M. A. (1964). Positive Solutions of Operator Equations. Groningen: P.Noordhoff Ltd. pp. 381 pp. 
5. Krasnosel'skii, M. A.; Lifshits, Je.A.; Sobolev, A.V. (1990). Positive Linear Systems: The method of positive operators. Sigma Series in Applied Mathematics. 5. Berlin: Helderman Verlag. pp. 354 pp. 
6. Henryk Minc, Nonnegative matrices, John Wiley&Sons, New York, 1988, ISBN 0-471-83966-3
7. Seneta, E. Non-negative matrices and Markov chains. 2nd rev. ed., 1981, XVI, 288 p., Softcover Springer Series in Statistics. (Originally published by Allen & Unwin Ltd., London, 1973) ISBN 978-0-387-29765-1
8. Richard S. Varga 2002 Matrix Iterative Analysis, Second ed. (of 1962 Prentice Hall edition), Springer-Verlag.

• Nicolas Gillis: Nonnegative Matrix Factorization, SIAM, ISBN 978-1-611976-40-3 (2020).
• Andrzej Cichocki; Rafel Zdunek; Anh Huy Phan; Shun-ichi Amari: Nonnegative Matrix and Tensor Factorizations: Applications to Exploratory Multi-way Data Analysis and Blind Source Separation, John Wiley & Sons, ISBN 978-0-470-74666-0 (2009).