円柱座標変換

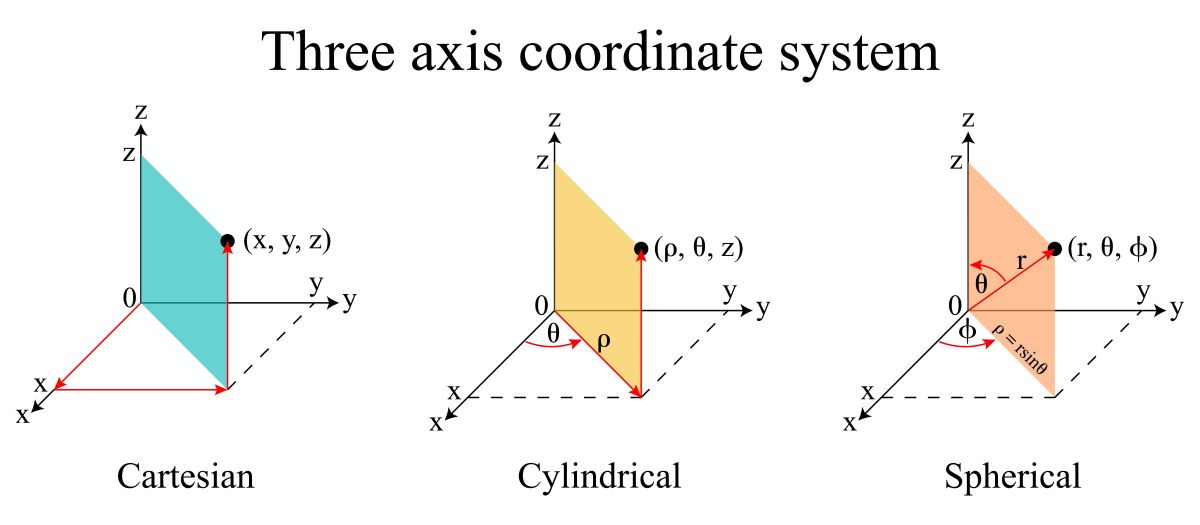
円柱座標変換（えんちゅうざひょうへんかん）とは、3次元ユークリッド空間 （数ベクトル空間)の、非線形な座標変換の一つである。円柱座標変換の逆写像のことを、円柱座標系という。円柱座標系は、極座標系の一種である。

円柱座標変換は、電子レンズなど、軸対称な系の計算によく用いられる。

定義

定義

円柱座標変換Φとは、

${\displaystyle \left({\begin{matrix}x\\y\\z\\\end{matrix}}\right)=\Phi (r,\theta ,\zeta )=\left({\begin{matrix}r\cos \theta \\r\sin \theta \\\zeta \\\end{matrix}}\right)}$　　(1-1-1)

で表される、r -θ-ζ空間からx -y -z 空間への多変数ベクトル値関数のことである。式（1-1-1）で定義されたΦに相似変換、場合によっては正則なアフィン変換を施したものも、円柱座標変換ということがあるので、特に混乱が生じる場合には（1-1-1）で定義されたΦを標準的な円柱座標変換ということにする。

r-θ-ζ空間、x-y-z空間の正体

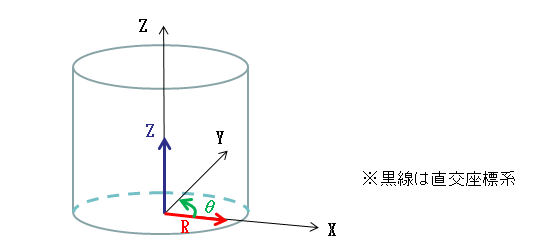
数学的には、r -θ-ζ空間、x -y -z 空間は、共に3次元実数ベクトル空間（${\displaystyle \mathbb {R} ^{3}}$）である。r -θ-ζ空間においては、第一軸方向をr 方向（r 軸）、第二軸方向をθ方向（θ軸）、第三軸方向をζ方向（ζ軸）とする。x -y -z 空間においても同様に、第一軸方向をx 方向（x 軸）、第二軸方向をy 方向（y 軸）、第三軸をz 方向（z軸）とする。この三軸によって定まる座標系を、「x -y -z 空間の標準座標系」（O-xyz 系）という。

定義域

式(1-1-1)の円柱座標変換Φ はr -θ-ζ空間のすべての点において、矛盾なく定義がされている。例えば、

${\displaystyle \Phi (-3,2\pi ,7)=\left({\begin{matrix}-3\\0\\7\end{matrix}}\right)}$　　(1-3-1)

のように、どのような (r, θ, ζ) に対しても、ただ一つの行き先を定めることができる。

しかし、本記事では特段の断りがない限り、Φ の定義域は式(1-3-2) に定める領域 V に制限されているものとする。V は、r -θ-ζ の部分集合であり、閉集合である（開集合ではない）。

${\displaystyle V=\left\{\left.{\begin{pmatrix}r\\\theta \\\zeta \end{pmatrix}}\left|\ {\begin{array}{l}0\leq r\\0\leq \theta \leq 2\pi \\-\infty <\zeta <\infty \end{array}}\right.\right\}\right.}$　　(1-3-2)

つまり、Φ に代入されるものは、

${\displaystyle \left\{{\begin{array}{l}0\leq r\\0\leq \theta \leq 2\pi \\-\infty <\zeta <\infty \end{array}}\right.}$　　(1-3-3)

のすべての条件を満たす点全てに限って考えることにする。

Φ の定義域を式(1-3-2) の V に制限してもよい理由は、全射性が保たれていることによる。

円柱座標系との関係

x -y -z 空間に、標準座標系（O-xyz 系；「r -θ-ζ空間、x -y -z 空間の正体」の項参照）が定められているとする。このとき、円柱座標系P とは、

${\displaystyle \left({\begin{matrix}r\\\theta \\\zeta \\\end{matrix}}\right)=P(x,y,z)=}$${\displaystyle \left({\begin{matrix}{\sqrt {{{x}^{2}} {{y}^{2}}}}\\\theta (x,y,z)\\z\\\end{matrix}}\right)}$　　(1-4-1)

で表される、x -y -z からr -θ-ζ空間への多変数ベクトル値関数のことである。但し、θ(x , y , z) は、以下の定義式(1-4-2)で与えられるスカラー値関数である。θ(x , y , z) の定義域はx -y -z 空間の原点以外である。その他の成分は、x -y -z 空間全域で定義されている。従って、円柱座標系P の定義域は、x -y -z 空間の原点以外である。

${\displaystyle \theta (x,y,z)=\left\{{\begin{matrix}{{\tan }^{-1}}(y/x)&(x>0,y>0)\\{\frac {\pi }{2}}&(x=0,y>0)\\\pi {{\tan }^{-1}}(y/x)&(x<0)\\{\frac {3\pi }{2}}&(x=0,y<0)\\2\pi {{\tan }^{-1}}(y/x)&(x=0,y<0)\\\end{matrix}}\right.}$　　(1-4-2)

円柱座標系は、以下の手順で、幾何学的に理解することもできる。

• 任意の点Pからxy平面に下した垂線の足をQとする。
• 線分OQの長さをrとする。
• 線分QPの長さをζとする。
• x軸と線分OQのなす角度をθとする。

また、円柱座標系と円柱座標変換は、相互に逆変換となっている。

微分

微分

円柱座標変換の偏導関数は、

${\displaystyle {\frac {\partial \Phi }{\partial r}}(r,\theta ,\zeta )=\left({\begin{matrix}\cos \theta \\\sin \theta \\0\\\end{matrix}}\right)}$　　(2-1-1)

${\displaystyle {\frac {\partial \Phi }{\partial \theta }}(r,\theta ,\zeta )=\left({\begin{matrix}-r\sin(\theta )\\r\cos(\theta )\\0\\\end{matrix}}\right)}$　　(2-1-2)

${\displaystyle {\frac {\partial \Phi }{\partial \zeta }}(r,\theta ,\zeta )=\left({\begin{matrix}0\\0\\1\\\end{matrix}}\right)}$　　(2-1-3)

である。これらの定義域は、r -θ-ζ空間全域である。

従って、円柱座標変換の点 (r , θ, ζ) におけるヤコビ行列J Φ(r , θ, ζ) およびヤコビアン det(J Φ(r , θ, ζ)) は以下のようになる。ヤコビ行列、ヤコビアン共に定義域はr -θ-ζ空間全域である。

${\displaystyle {{J}{\Phi }}(r,\theta ,\zeta )=\left({\begin{matrix}\cos \theta &-r\sin \theta &0\\\sin \theta &r\cos \theta &0\\0&0&1\\\end{matrix}}\right)}$　　(2-1-4)

${\displaystyle \det({{J}{\Phi }}(r,\theta ,\zeta ))=\left|{\begin{matrix}\cos \theta &-r\sin \theta &0\\\sin \theta &r\cos \theta &0\\0&0&1\\\end{matrix}}\right|=r}$　　(2-1-5)

従って、円座標のときと同じく、特異点（ヤコビアンが 0 となる点）は、r = 0 となる点全て、つまり (0, θ, ζ) の形であらわされる点全てである。これらの点は全てx -y -z 空間上ではz 軸に移る。

法線

標準的な円柱座標変換Φに対し、N_r , N_θ , N_ζ を以下のように定義し、それぞれr 法線、θ法線、ζ法線と呼ぶ。これらの定義域は、r -θ-ζ空間全域である。

${\displaystyle {{\mathbf {N} }_{r}}(r,\theta ,\zeta )={\frac {\left({\frac {\partial \Phi }{\partial \theta }}(r,\theta ,\zeta )\right)\times \left({\frac {\partial \Phi }{\partial \zeta }}(r,\theta ,\zeta )\right)}{\left\|\left({\frac {\partial \Phi }{\partial \theta }}(r,\theta ,\zeta )\right)\times \left({\frac {\partial \Phi }{\partial \zeta }}(r,\theta ,\zeta )\right)\right\|}}=\left({\begin{matrix}\cos \theta \\\sin \theta \\0\\\end{matrix}}\right)}$　　(2-2-1)

${\displaystyle {{\mathbf {N} }_{\theta }}(r,\theta ,\zeta )={\frac {\left({\frac {\partial \Phi }{\partial \zeta }}(r,\theta ,\zeta )\right)\times \left({\frac {\partial \Phi }{\partial r}}(r,\theta ,\zeta )\right)}{\left\|\left({\frac {\partial \Phi }{\partial \zeta }}(r,\theta ,\zeta )\right)\times \left({\frac {\partial \Phi }{\partial r}}(r,\theta ,\zeta )\right)\right\|}}=\left({\begin{matrix}-\sin \theta \\\cos \theta \\0\\\end{matrix}}\right)}$　　(2-2-2)

${\displaystyle {{\mathbf {N} }_{z}}(r,\theta ,\zeta )={\frac {\left({\frac {\partial \Phi }{\partial r}}(r,\theta ,\zeta )\right)\times \left({\frac {\partial \Phi }{\partial \theta }}(r,\theta ,\zeta )\right)}{\left\|\left({\frac {\partial \Phi }{\partial r}}(r,\theta ,\zeta )\right)\times \left({\frac {\partial \Phi }{\partial \theta }}(r,\theta ,\zeta )\right)\right\|}}=\left({\begin{matrix}0\\0\\1\\\end{matrix}}\right)}$　　(2-2-3)

ここで、“×”はベクトル積を意味する。これらの幾何学的な意味は、後述するが、幾何学的な意味でも、これらは法線になっている。

円柱と円柱座標

この節では、後述の説明のために記号を定義する。

円柱と円柱座標

M を、${\displaystyle x-y-z}$空間で半径r₀ 、高さz₀のふたと底のある、中身のつまった円柱（以降「ソリッド円柱」と呼ぶ）とする。式で書くと

${\displaystyle M=\left\{\left.\left({\begin{matrix}x\\y\\z\\\end{matrix}}\right)\ \left|{\begin{matrix}{{x}^{2}} {{y}^{2}}\leq {{r}_{0}}\\0\leq z\leq {{z}_{0}}\\\end{matrix}}\right.\right\}\right.}$　　(3-1-1)

である。さらに、「ソリッド円柱」に該当するもの全ては、このM に相似変換を加えれば集合として実現できるので、以下は、M のみについて考える。

次に、このM を、円柱座標変換Φとr -θ-ζ空間内の直方体（六面体）L を用いてパラメータ付け（パラメトライズ）することを考える。r -θ-ζ空間内の直方体L を

${\displaystyle L=\left\{\left.\left({\begin{matrix}r\\\theta \\\zeta \\\end{matrix}}\right)\ \left|{\begin{matrix}0\leq r\leq {{r}_{0}}\\0\leq \theta \leq 2\pi \\0\leq \zeta \leq {{z}_{0}}\\\end{matrix}}\right.\right\}\right.}$　　(3-1-2)

と定義する。L の3辺の長さはそれぞれ、r₀ , θ₀ , 2πである。M は、L のΦによる像集合である。すなわち

${\displaystyle M=\Phi (L)}$　　(3-1-3)

である。上式の等号は、集合として等しいことを意味する。

円柱表面

式(3-1-1)のソリッド円柱M の表面を${\displaystyle \partial M}$と書き、円柱表面、円筒面、M の表面、あるいはM の境界面と呼ぶ。表面∂M は、以下のΔ₁ , Δ₂ , Δ₃ に分割することができる。

${\displaystyle {{\Delta }_{1}}=\left\{\left.\left({\begin{matrix}x\\y\\z\\\end{matrix}}\right)\ \left|{\begin{matrix}{{x}^{2}} {{y}^{2}}\leq {{r}_{0}}\\z=0\\\end{matrix}}\right.\right\}\right.}$　　(3-2-1)

${\displaystyle {{\Delta }_{2}}=\left\{\left.\left({\begin{matrix}x\\y\\z\\\end{matrix}}\right)\ \left|{\begin{matrix}{{x}^{2}} {{y}^{2}}={{r}_{0}}\\0\leq z\leq {{z}_{0}}\\\end{matrix}}\right.\right\}\right.}$　　(3-2-2)

${\displaystyle {{\Delta }_{3}}=\left\{\left.\left({\begin{matrix}x\\y\\z\\\end{matrix}}\right)\ \left|{\begin{matrix}{{x}^{2}} {{y}^{2}}\leq {{r}_{0}}\\z={{z}_{0}}\\\end{matrix}}\right.\right\}\right.}$　　(3-2-3)

Δ₁ , Δ₂ , Δ₃ をそれぞれ、下面、側面、上面という。

逆に言うと、Δ₁ , Δ₂ , Δ₃ を貼り合わせたものが∂M である。集合演算を用いると、

${\displaystyle \partial M={\Delta }_{1}\cup {\Delta }_{2}\cup {\Delta }_{3}}$　　(3-2-4)

のようになる。

次に、Δ₁ , Δ₂ , Δ₃ を、円柱座標変換を利用してパラメトライズすることを考える。D₁ , D₂ , D₃ を以下のように定める。

${\displaystyle {{D}_{1}}=\left\{\left.\left({\begin{matrix}r\\\theta \\\end{matrix}}\right)\ \left|{\begin{matrix}0\leq r\leq {{r}_{0}}\\0\leq \theta \leq 2\pi \\\end{matrix}}\right.\right\}\right.}$　　(3-2-5)

${\displaystyle {{D}_{2}}=\left\{\left.\left({\begin{matrix}\theta \\\zeta \\\end{matrix}}\right)\ \left|{\begin{matrix}0\leq \theta \leq 2\pi \\0\leq \zeta \leq {{z}_{0}}\\\end{matrix}}\right.\right\}\right.}$　　(3-2-6)

${\displaystyle {{D}_{3}}=\left\{\left.\left({\begin{matrix}r\\\theta \\\end{matrix}}\right)\ \left|{\begin{matrix}0\leq r\leq {{r}_{0}}\\0\leq \theta \leq 2\pi \\\end{matrix}}\right.\right\}\right.}$　　(3-2-7)

D₁ , D₂ , D₃ は、それぞれr -θ平面、θ-ζ平面、r -θ平面の部分集合となっている。また、D₁ とD₃ は集合として全く等しいものである。

また、x -y -z 空間に値を取るベクトル値関数I₁ , I₂ , I₃ を以下のように定義する。I₁ , I₂ , I₃ の定義域は、本来的にはそれぞれr -θ平面、θ-ζ平面、r -θ平面であるが、ここでは、それぞれの定義域をD₁ , D₂ , D₃ に制限して考えることにする。これらI₁ , I₂ , I₃ を、それぞれΔ₁ , Δ₂ , Δ₃ のパラメータと呼ぶ。

${\displaystyle \left({\begin{matrix}x\\y\\z\\\end{matrix}}\right)={{\mathbf {I} }_{1}}(r,\theta )=\Phi (r,\theta ,0)=\left({\begin{matrix}r\cos \theta \\r\sin \theta \\0\\\end{matrix}}\right)}$　　(3-2-8)

${\displaystyle \left({\begin{matrix}x\\y\\z\\\end{matrix}}\right)={{\mathbf {I} }_{2}}(\theta ,\zeta )=\Phi ({{r}_{0}},\theta ,\zeta )=\left({\begin{matrix}{{r}_{0}}\cos \theta \\{{r}_{0}}\sin \theta \\\zeta \\\end{matrix}}\right)}$　　(3-2-9)

${\displaystyle \left({\begin{matrix}x\\y\\z\\\end{matrix}}\right)={{\mathbf {I} }_{3}}(r,\theta )=\Phi (r,\theta ,{{z}_{0}})=\left({\begin{matrix}r\cos(-\theta )\\r\sin(-\theta )\\{{z}_{0}}\\\end{matrix}}\right)}$　　(3-2-10)

Δ₁ , Δ₂ , Δ₃ は、それぞれD₁ , D₂ , D₃ のI₁ , I₂ , I₃ による像集合となっている：

${\displaystyle \left\{{\begin{array}{*{35}{l}}{{\Delta }_{1}}={{\mathbf {I} }_{1}}({{D}_{1}})\\{{\Delta }_{2}}={{\mathbf {I} }_{2}}({{D}_{2}})\\{{\Delta }_{3}}={{\mathbf {I} }_{3}}({{D}_{3}})\\\end{array}}\right.}$　　(3-2-11)

ここで、“＝”は集合としての等号である。例えば、Δ₁ = I₁(D₁) とは、Δ₁ とI₁ (D₁) が集合として等しいことを意味している。

Δ₁ , Δ₂ , Δ₃ それぞれの法線ベクトルを、N_Δ1 , N_Δ2 , N_Δ3と書く：

${\displaystyle {{\mathbf {N} }_{{\Delta }_{1}}}(r,\theta )={\frac {\left({\frac {\partial \Phi }{\partial r}}(r,\theta ,0)\right)\times \left({\frac {\partial \Phi }{\partial \theta }}(r,\theta ,0)\right)}{\left\|\left({\frac {\partial \Phi }{\partial r}}(r,\theta ,0)\right)\times \left({\frac {\partial \Phi }{\partial \theta }}(r,\theta ,0)\right)\right\|}}={{\mathbf {N} }_{\zeta }}(r,\theta ,{{\zeta }_{0}})=\left({\begin{matrix}0\\0\\1\\\end{matrix}}\right)}$　　(3-2-12)

${\displaystyle {{\mathbf {N} }_{{\Delta }_{2}}}(\theta ,\zeta )={\frac {\left({\frac {\partial \Phi }{\partial \zeta }}({r}_{0},\theta ,\zeta )\right)\times \left({\frac {\partial \Phi }{\partial r}}(r,\theta ,\zeta )\right)}{\left\|\left({\frac {\partial \Phi }{\partial \zeta }}({r}_{0},\theta ,\zeta )\right)\times \left({\frac {\partial \Phi }{\partial r}}(r,\theta ,\zeta )\right)\right\|}}={{\mathbf {N} }_{r}}(r,\theta ,\zeta )=\left({\begin{matrix}-\sin \theta \\\cos \theta \\0\\\end{matrix}}\right)}$　　(3-2-13)

${\displaystyle {{\mathbf {N} }_{{\Delta }_{3}}}(r,\theta )={\frac {\left({\frac {\partial \Phi }{\partial r}}(r,\theta ,\zeta _{0})\right)\times \left(-\left({\frac {\partial \Phi }{\partial \theta }}\right)(r,\theta ,\zeta _{0})\right)}{\left\|\left({\frac {\partial \Phi }{\partial r}}(r,\theta ,\zeta _{0})\right)\times \left(-\left({\frac {\partial \Phi }{\partial \theta }}\right)(r,\theta ,\zeta _{0})\right)\right\|}}=-{{\mathbf {N} }_{\zeta }}(r,\theta ,\zeta _{0})=\left({\begin{matrix}0\\0\\-1\\\end{matrix}}\right)}$　　(3-2-14)

N_Δ1 , N_Δ2 , N_Δ3 の定義域は、それぞれD₁ , D₂ , D₃ である。ここで、N_θに平行なものがないことに注意されたい。

ベクトル場

x -y -z 空間で定義されたベクトル場X をx -y -z 座標系について表示すると

${\displaystyle \mathbf {X} (x,y,z)=\left({\begin{array}{c}{X}_{x}(x,y,z)\\{X}_{y}(x,y,z)\\{X}_{z}(x,y,z)\\\end{array}}\right)}$　　(4-1-1)

となる。これを円柱座標表示に変換することを考える。まず、スカラー値関数X_r (r , θ, ζ) , X_θ (r , θ, ζ) , X_ζ (r , θ, ζ) を、

${\displaystyle \left\{{\begin{matrix}{{X}_{r}}=\mathbf {X} \cdot {{\mathbf {N} }_{r}}\\{{X}_{\theta }}=\mathbf {X} \cdot {{\mathbf {N} }_{\theta }}\\{{X}_{\zeta }}=\mathbf {X} \cdot {{\mathbf {N} }_{z}}\\\end{matrix}}\right.}$　(4-1-2)

と定義する。正確に書くと

${\displaystyle \left\{{\begin{matrix}X_{r}(r,\theta ,\zeta )=\mathbf {X} \left(\Phi (r,\theta ,\zeta )\right)\cdot {\mathbf {N} _{r}}(r,\theta ,\zeta )\\X_{\theta }(r,\theta ,\zeta )=\mathbf {X} \left(\Phi (r,\theta ,\zeta )\right)\cdot {\mathbf {N} _{\theta }}(r,\theta ,\zeta )\\X_{\zeta }(r,\theta ,\zeta )=\mathbf {X} \left(\Phi (r,\theta ,\zeta )\right)\cdot {\mathbf {N} _{\zeta }}(r,\theta ,\zeta )\end{matrix}}\right.}$　(4-1-3)

である。ここで、・は内積を意味する。定義式(4-1-3)から明らかなように、これらの定義域はr -θ-ζ空間全域（r = 0 となる点を含む）である。

ここで以下が成立する。”${\displaystyle \circ }$”は、合成関数の意味である。

${\displaystyle \left\{{\begin{array}{*{35}{l}}{{X}_{r}}=({X}_{x}\circ \Phi )\cos \theta ({X}_{y}\circ \Phi )\sin \theta \\{{X}_{\theta }}=-({X}_{x}\circ \Phi )\sin \theta ({X}_{y}\circ \Phi )\cos \theta \\{{X}_{\zeta }}={{X}_{z}\circ \Phi }\\\end{array}}\right.}$　　　(4-1-4)

またはこれを逆に解くと

${\displaystyle \left\{{\begin{array}{*{35}{l}}{{X}_{x}}\circ \Phi ={{X}_{r}}\cos \theta -{{X}_{\theta }}\sin \theta \\{{X}_{y}}\circ \Phi ={{X}_{r}}\sin \theta {{X}_{\theta }}\cos \theta \\{{X}_{z}}\circ \Phi ={{X}_{\zeta }}\\\end{array}}\right.}$　　　(4-1-5)

が分かる。

また、次の等式がr = 0 となる点を含むすべての (r , θ, ζ) に対して成立する。

${\displaystyle \mathbf {X} (\Phi (r,\theta ,z))=({{X}_{r}}{{\mathbf {N} }_{r}})(r,\theta ,z) ({{X}_{\theta }}{{\mathbf {N} }_{\theta }})(r,\theta ,z) ({{X}_{z}}{{\mathbf {N} }_{z}})(r,\theta ,z)}$　　　(4-1-6)

式(4-1-6)を、ベクトル場の円柱座標表示という。より正確な言い方をすると、「x -y -z 空間で定義されたベクトル場X の円柱座標表示」という。

積分

体積分

ここではx -y -z 空間で定義されたスカラー値関数f の、式(3-1-1)の円柱M 内部での積分

${\displaystyle {\int }_{M}f\ dxdydz}$　　(5-1-1)

の計算方法を説明する。円柱M について

${\displaystyle M=\left\{\left.\left({\begin{matrix}x\\y\\z\\\end{matrix}}\right)\ \left|{\begin{matrix}{{x}^{2}} {{y}^{2}}\leq {{r}_{0}}\\0\leq z\leq {{z}_{0}}\\\end{matrix}}\right.\right\}\right.}$${\displaystyle =\left\{\left.\left({\begin{matrix}x\\y\\z\\\end{matrix}}\right)\ \left|{\begin{matrix}-r_{0}\leq x\leq r_{0}\\-{\sqrt {r_{0}^{2}-x^{2}}}\leq y\leq {\sqrt {r_{0}^{2}-x^{2}}}\\0\leq z\leq z_{0}\end{matrix}}\right.\right\}\right.}$　　(5-1-2)

が成立することに注意すると、f の積分は以下のように累次積分に帰着されることが分かる。

${\displaystyle \int _{M}{f\ dxdydz}=\int _{z=-{{z}_{0}}}^{z={{z}_{0}}}{\int _{x=-{{r}_{0}^{}}}^{x=r}{\int _{y=-{\sqrt {{{r}_{0}^{2}}-{{x}^{2}}}}}^{y=\ {\sqrt {{{r}_{0}^{2}}-{{x}^{2}}}}}{\ f(x,y,z)\ dxdydz}}}}$　　(5-1-3)

また、式(3-1-2)の直方体L に対しM = Φ(L )（式(3-1-3)）であることと、ヤコビアン（式(2-1-5)）に注意して、積分の変数変換公式を用いると、

${\displaystyle {\begin{aligned}\int _{M}^{}{f\ dxdydz}&=\int _{L}{(f\circ \Phi )\cdot (\det J\Phi )\ drd\theta d\zeta }\\&={\int _{r=0}^{r={{r}_{0}}}{\int _{\theta =0}^{\theta =2\pi }\int _{\zeta =-{{z}_{0}}}^{\zeta ={{z}_{0}}}{\ r\cdot \left(f\circ \Phi \right)(r,\theta ,\zeta )\ drd\theta d\zeta }}}\end{aligned}}}$　　(5-1-4)

が分かる。

以上、まとめると、

${\displaystyle {\begin{aligned}\int _{M}{f\ dxdydz}&=\int _{z=-z_{0}}^{z=z_{0}}{\int _{x=-r_{0}}^{x=r}{\int _{y=-{\sqrt {r_{0}^{2}-x^{2}}}}^{y=\ {\sqrt {r_{0}^{2}-x^{2}}}}{\ f(x,y,z)\ dxdydz}}}\\&=\int _{r=0}^{r=r_{0}}{\int _{\theta =0}^{\theta =2\pi }{\int _{\zeta =-z_{0}}^{\zeta =z_{0}}{\ r\cdot \left(f\circ \Phi \right)(r,\theta ,\zeta )\ drd\theta d\zeta }}}\end{aligned}}}$　(5-1-5)

がわかる。

面積分

ここでは、ベクトル場の円柱表面∂M 上での面積分の計算方法を説明する。

x -y -z 空間で定義されたベクトル場X に対して、円柱面∂M 上の面積分を

${\displaystyle \int _{\partial \mathbf {M} }{\mathbf {X} }=\int _{{\Delta }_{1}}{\mathbf {X} } \int _{{\Delta }_{2}}{\mathbf {X} } \int _{{\Delta }_{3}}{\mathbf {X} }}$　　　(5-2-1)

で定める。但し、右辺の各項は

${\displaystyle \int _{{\Delta }_{1}}{\mathbf {X} }=\int _{r=0}^{r={{r}_{0}}}{\int _{\theta =0}^{\theta =2\pi }{\left(\mathbf {X} \cdot \left({\frac {\partial {{\mathbf {I} }_{1}}}{\partial r}}\times {\frac {\partial {{\mathbf {I} }_{1}}}{\partial \theta }}\right)\right)}}\ d\theta dr}$　　　(5-2-2)

${\displaystyle \int _{{\Delta }_{2}}{\mathbf {X} }=\int _{\zeta =0}^{\zeta ={{\zeta }_{0}}}{\int _{\theta =0}^{\theta =2\pi }{\left(\mathbf {X} \cdot \left({\frac {\partial {{\mathbf {I} }_{2}}}{\partial \theta }}\times {\frac {\partial {{\mathbf {I} }_{2}}}{\partial \zeta }}\right)\right)}}\ d\theta d\zeta }$　　　(5-2-3)

${\displaystyle \int _{{\Delta }_{3}}{\mathbf {X} }=\int _{r=0}^{r={{r}_{0}}}{\int _{\theta =0}^{\theta =2\pi }{\left(\mathbf {X} \cdot \left({\frac {\partial {{\mathbf {I} }_{3}}}{\partial r}}\times {\frac {\partial {{\mathbf {I} }_{3}}}{\partial \theta }}\right)\right)}}\ d\theta dr}$　　　(5-2-4)

である。ここで、

${\displaystyle \mathbf {X} \cdot \left({\frac {\partial {{\mathbf {I} }_{1}}}{\partial r}}\times {\frac {\partial {{\mathbf {I} }_{1}}}{\partial \theta }}\right)=\mathbf {X} \cdot {\frac {\left({\frac {\partial {{\mathbf {I} }_{1}}}{\partial r}}\times {\frac {\partial {{\mathbf {I} }_{1}}}{\partial \theta }}\right)}{\left\|{\frac {\partial {{\mathbf {I} }_{1}}}{\partial r}}\times {\frac {\partial {{\mathbf {I} }_{1}}}{\partial \theta }}\right\|}}\left\|{\frac {\partial {{\mathbf {I} }_{1}}}{\partial r}}\times {\frac {\partial {{\mathbf {I} }_{1}}}{\partial \theta }}\right\|=\left(\mathbf {X} \cdot {{\mathbf {N} }_{\zeta }}\right)\left\|{\frac {\partial {{\mathbf {I} }_{1}}}{\partial r}}\times {\frac {\partial {{\mathbf {I} }_{1}}}{\partial \theta }}\right\|=r\cdot {{X}_{\zeta }}}$　(5-2-5)

同様に、

${\displaystyle \mathbf {X} \cdot \left({\frac {\partial {{\mathbf {I} }_{2}}}{\partial \theta }}\times {\frac {\partial {{\mathbf {I} }_{2}}}{\partial \zeta }}\right)={{r}_{0}}\cdot {{X}_{r}}}$　　　(5-2-6)

${\displaystyle \mathbf {X} \cdot \left({\frac {\partial {{\mathbf {I} }_{3}}}{\partial \theta }}\times {\frac {\partial {{\mathbf {I} }_{3}}}{\partial \zeta }}\right)=-r\cdot {{X}_{\zeta }}}$　　　(5-2-7)

なので、

${\displaystyle \int _{{\Delta }_{1}}{\mathbf {X} }=\int _{r=0}^{r={{r}_{0}}}{\int _{\theta =0}^{\theta =2\pi }{r\cdot {{X}_{\zeta }}(r,\theta ,{{\zeta }_{0}})}}\ d\theta dr}$　　　(5-2-8)

${\displaystyle \int _{{\Delta }_{2}}{\mathbf {X} }=\int _{\theta =0}^{\theta =2\pi }{{{r}_{0}}\cdot {{X}_{r}}({{r}_{0}},\theta ,\zeta )}\ d\theta d\zeta }$　　　(5-2-9)

${\displaystyle \int _{{\Delta }_{3}}{\mathbf {X} }=\int _{r=0}^{r={{r}_{0}}}{\int _{\theta =0}^{\theta =2\pi }{-r\cdot {{X}_{\zeta }}(r,\theta ,0)}}\ d\theta dr}$　　　(5-2-10)

である。従って、

${\displaystyle \int _{\partial \mathbf {M} }{\mathbf {X} }=\int _{r=0}^{r={{r}_{0}}}{\int _{\theta =0}^{\theta =2\pi }r{\left({{X}_{\zeta }}(r,\theta ,{{\zeta }_{0}})-{{X}_{\zeta }}(r,\theta ,0)\right)d\theta dr}}\ \ \int _{\zeta =0}^{\zeta ={{\zeta }_{0}}}{\int _{\theta =0}^{\theta =2\pi }{{{r}_{0}}{{X}_{r}}({{r}_{0}},\theta ,\zeta )}}\ d\theta d\zeta }$　　　(5-2-11)

が分かる。

ガウスの発散定理

x -y -z 空間で定義されたベクトル場X に対して、

${\displaystyle \int _{\partial M}{\mathbf {X} }=\int _{M}{\operatorname {div} {\textbf {X}}\ dxdydz}}$　　　(5-3-1)

が成立する。この事実を、円柱面におけるガウスの発散定理という。ここで、

${\displaystyle \operatorname {div} \mathbf {X} =\left({\frac {\partial {{X}_{x}}}{\partial x}}\right) \left({\frac {\partial {{X}_{y}}}{\partial y}}\right) \left({\frac {\partial {{X}_{z}}}{\partial z}}\right)}$　　　(5-3-2)

はベクトル場X の発散である。以下、証明を行う。

証明の準備

(5-1-5)、(5-2-2)、(5-2-3)、(5-2-4)より、

${\displaystyle \int _{\zeta =0}^{\zeta ={{\zeta }_{0}}}{\int _{\theta =0}^{\theta =2\pi }{{{r}_{0}}{{X}_{r}}({{r}_{0}},\theta ,\zeta )}}\ d\theta d\zeta =\int _{M}{\left(\left({\frac {\partial {{X}_{x}}}{\partial x}}\right) \left({\frac {\partial {{X}_{y}}}{\partial y}}\right)\ \right)dxdydz}}$　　　(5-3-3)

${\displaystyle \int _{r=0}^{r={{r}_{0}}}{\int _{\theta =0}^{\theta =2\pi }{r\left({{X}_{\varsigma }}(r,\theta ,{{\zeta }_{0}})-{{X}_{\zeta }}(r,\theta ,0)\right)}}\ \ d\theta dr=\int _{M}{\left({\frac {\partial {{X}_{z}}}{\partial z}}\right)dxdydz}}$　　　(5-3-4)

を示せばよいことがわかる。

x,y成分についての証明

まず、式(5-3-3)を示す。

x -y 平面上の曲線c (t ) を、

${\displaystyle c(t)=\left({\begin{matrix}{{r}_{0}}\cos t\\{{r}_{0}}\sin t\\\end{matrix}}\right)}$　　　(5-3-5)

とする。また、変数z を固定して考えることで、x -y 平面上の二次元ベクトル場

${\displaystyle \mathbf {A} \left(x,y\right)=\left({\begin{matrix}a\left(x,y\right)\\b\left(x,y\right)\\\end{matrix}}\right)=\left({\begin{matrix}-{{X}_{y}}(x,y,z)\\{{X}_{x}}(x,y,z)\\\end{matrix}}\right)}$　　　(5-3-6)

を考える。また、平面曲線と、二次元ベクトル場に対しては、(5-3-6)に対するグリーンの定理：

${\displaystyle \int _{c}^{}{A}=\int _{x=-{{r}_{0}}}^{x={{r}_{0}}}{\int _{-{\sqrt {{{r}_{0}}^{2}-{{x}^{2}}}}}^{\sqrt {{{r}_{0}}^{2}-{{x}^{2}}}}{\left({\frac {\partial b}{\partial x}}-{\frac {\partial a}{\partial y}}\right)dxdy}}}$　　　(5-3-7)

が成立することは、既知とする。

このとき

${\displaystyle {\begin{aligned}\int _{\theta =0}^{\theta =2\pi }{r_{0}X_{r}(r_{0},\theta ,\zeta )}\ d\theta &=\int _{\theta =0}^{\theta =2\pi }{\left((X_{x}\circ \Phi )r_{0}\cos \theta (X_{y}\circ \Phi )r_{0}\sin \theta \right)}\ d\theta \\&=\int _{\theta =0}^{\theta =2\pi }{\left(X_{x}(r_{0}\cos \theta ,r_{0}\sin \theta ,\zeta )r_{0}\cos \theta X_{y}(r_{0}\cos \theta ,r_{0}\sin \theta ,\zeta )r_{0}\sin \theta \right)}\ d\theta \\&=\int _{t=0}^{t=2\pi }{\left({\begin{matrix}-X_{y}(r_{0}\cos t,r_{0}\sin t,\zeta )\\X_{x}(r_{0}\cos t,r_{0}\sin t,\zeta )\\\end{matrix}}\right)}\ \cdot \left({\begin{matrix}-r_{0}\sin t\\r_{0}\cos t\\\end{matrix}}\right)dt\\&=\int _{t=0}^{t=2\pi }{\left({\begin{matrix}a\circ c(t)\\b\circ c(t)\\\end{matrix}}\right)}\ \cdot \left({\frac {dc}{dt}}\right)dt\\&=\int _{x=-{{r}_{0}}}^{x={{r}_{0}}}{\int _{y=-{\sqrt {{{r}_{0}}^{2}-{{x}^{2}}}}}^{y={\sqrt {{{r}_{0}}^{2}-{{x}^{2}}}}}{\left({\frac {\partial b}{\partial x}}-{\frac {\partial a}{\partial y}}\right)dydx}}\\&=\int _{x=-{{r}_{0}}}^{x={{r}_{0}}}{\int _{y=-{\sqrt {{{r}_{0}}^{2}-{{x}^{2}}}}}^{y={\sqrt {{{r}_{0}}^{2}-{{x}^{2}}}}}{\left({\frac {\partial {{X}_{x}}(x,y,z)}{\partial x}} {\frac {\partial {{X}_{y}}(x,y,z)}{\partial y}}\right)dydx}}\end{aligned}}}$　　　(5-3-8)

が成り立つ。従って、

${\displaystyle \int _{\zeta =0}^{\zeta ={{\zeta }_{0}}}{\int _{\theta =0}^{\theta =2\pi }{{{X}_{r}}({{r}_{0}},\theta ,\zeta )}}\ d\theta d\zeta =\int _{z=0}^{z={{\zeta }_{0}}}{\int _{\theta =0}^{\theta =2\pi }{{{X}_{r}}({{r}_{0}},\theta ,z)}}\ d\theta dz}$

${\displaystyle \int _{z=0}^{z={{\zeta }_{0}}}{\int _{x=-r}^{x=r}{\int _{y=-{\sqrt {{{r}^{2}}-{{x}^{2}}}}}^{y={\sqrt {{{r}^{2}}-{{x}^{2}}}}}{\left({\frac {\partial {{X}_{x}}(x,y,z)}{\partial x}} {\frac {\partial {{X}_{y}}(x,y,z)}{\partial y}}\right)dydx}}}dz}$　　　(5-3-9)

z成分について

次に、

${\displaystyle \int _{r=0}^{r={{r}_{0}}}{\int _{\theta =0}^{\theta =2\pi }{r\left({{X}_{\varsigma }}(r,\theta ,{{\zeta }_{0}})-{{X}_{\zeta }}(r,\theta ,0)\right)}}\ \ d\theta dr=\int _{M}{\left({\frac {\partial {{X}_{z}}}{\partial z}}\right)dxdydz}}$　　　(5-3-10)

を示す。

${\displaystyle \int _{z=0}^{z={{\zeta }_{0}}}{{\frac {\partial {{X}_{\zeta }}(r,\theta ,\zeta )\ }{\partial \zeta }}d\zeta }={{X}_{\zeta }}(r,\theta ,{{\zeta }_{0}})-{{X}_{\zeta }}\ (r,\theta ,0)}$　　　(5-3-11)

なので、

${\displaystyle {\begin{aligned}\int _{r=0}^{r=r_{0}}{\int _{\theta =0}^{\theta =2\pi }{r\left(X_{\varsigma }(r,\theta ,\zeta _{0})-X_{\zeta }(r,\theta ,0)\right)\ \ d\theta }dr}&=\int _{r=0}^{r=r_{0}}{r\left(\int _{\theta =0}^{\theta =2\pi }{\left(X_{\varsigma }(r,\theta ,\zeta _{0})-X_{\zeta }(r,\theta ,0)\right)d\theta }\right)\ \ dr}\\&=\int _{r=0}^{r=r_{0}}{r\left(\int _{\theta =0}^{\theta =2\pi }{\int _{\zeta =0}^{\zeta =\zeta _{0}}{{\frac {\partial X_{\zeta }(r,\theta ,\zeta )}{\partial \zeta }}d\zeta }d\theta }\right)\ dr}\\&=\int _{r=0}^{r=r_{0}}{\int _{\theta =0}^{\theta =2\pi }{\int _{\zeta =0}^{\zeta =\zeta _{0}}{\left({\frac {\partial X_{\zeta }(r,\theta ,\zeta )}{\partial \zeta }}\right)rd\zeta }d\theta }dr}\\&=\int _{r=0}^{r=r_{0}}{\int _{\theta =0}^{\theta =2\pi }{\int _{\zeta =0}^{\zeta =\zeta _{0}}{\left(\left({\frac {\partial X_{z}}{\partial z}}\right){}^{\circ }\Phi (r,\theta ,\zeta )\right)rd\zeta }d\theta }dr}\\&=\int _{r=0}^{r=r_{0}}{\int _{\theta =0}^{\theta =2\pi }{\int _{\zeta =0}^{\zeta =\zeta _{0}}{\left(\left({\frac {\partial X_{z}}{\partial z}}\right){}^{\circ }\Phi (r,\theta ,\zeta )\right)\left(\det(J\Phi (r,\theta ,\zeta ))\right)d\zeta }d\theta }dr}\\&=\int _{z=0}^{z=\zeta _{0}}{\int _{x=-r}^{x=r}{\int _{y=-{\sqrt {r^{2}-x^{2}}}}^{y={\sqrt {r^{2}-x^{2}}}}{\left({\frac {\partial X_{z}(x,y,z)}{\partial z}}\right)dy}dx}dz}\end{aligned}}}$　　　(5-3-12)

スカラー関数に作用する微分作用素

x-y-z空間における偏微分

f を、x -y -z 空間で定義されたスカラー値関数とする。このとき、r ≠ 0 をみたす任意の (r , θ, ζ) に対して以下の(6-1-1)～(6-1-3)の等式が成立する：

${\displaystyle \left({\frac {\partial f}{\partial x}}\right)(\Phi (r,\theta ,\zeta ))=\cos \theta \left(\left({\frac {\partial (f\circ \Phi )}{\partial r}}\right)(r,\theta ,z)\right)-{\frac {\sin \theta }{r}}\left(\left({\frac {\partial (f\circ \Phi )}{\partial \theta }}\right)(r,\theta ,z)\right)}$　(6-1-1)

${\displaystyle \left({\frac {\partial f}{\partial y}}\right)(\Phi (r,\theta ,\zeta ))=\sin \theta \left(\left({\frac {\partial (f\circ \Phi )}{\partial r}}\right)(r,\theta ,z)\right) {\frac {\cos \theta }{r}}\left(\left({\frac {\partial (f\circ \Phi )}{\partial \theta }}\right)(r,\theta ,z)\right)}$　(6-1-2)

${\displaystyle \left({\frac {\partial f}{\partial z}}\right)(\Phi (r,\theta ,z))=\left({\frac {\partial (f\circ \Phi )}{\partial \zeta }}\right)(r,\theta ,z)}$　(6-1-3)

上記の3式は、しばしば略記的に以下のように表記される：

${\displaystyle \left\{{\begin{array}{*{35}{l}}\left({\frac {\partial f}{\partial x}}\right)=\cos \theta \left({\frac {\partial f}{\partial r}}\right)-{\frac {\sin \theta }{r}}\left({\frac {\partial f}{\partial \theta }}\right)\\\left({\frac {\partial f}{\partial y}}\right)=\sin \theta \left({\frac {\partial f}{\partial r}}\right) {\frac {\cos \theta }{r}}\left({\frac {\partial f}{\partial \theta }}\right)\\\left({\frac {\partial f}{\partial z}}\right)=\left({\frac {\partial f}{\partial \zeta }}\right)\\\end{array}}\right.}$　(6-1-4)

勾配作用素

勾配 grad ：

${\displaystyle {\begin{aligned}(\operatorname {grad} f)(x,y,z)&=\left({\begin{matrix}(\partial f/\partial x)(x,y,z)\\(\partial f/\partial y)(x,y,z)\\(\partial f/\partial z)(x,y,z)\\\end{matrix}}\right)\\&=\left(\left({\frac {\partial f}{\partial x}}\right)(x,y,z)\right)\left({\begin{matrix}1\\0\\0\\\end{matrix}}\right) \left(\left({\frac {\partial f}{\partial y}}\right)(x,y,z)\right)\left({\begin{matrix}0\\1\\0\\\end{matrix}}\right) \left(\left({\frac {\partial f}{\partial z}}\right)(x,y,z)\right)\left({\begin{matrix}0\\0\\1\\\end{matrix}}\right)\end{aligned}}}$ (6-2-1)

を円柱座標変換すると

．．．

以下、証明を行う。(grad f )(Φ(r , θ, ζ)) と、N_r (r , θ, ζ) の内積を取ると、

${\displaystyle {\begin{aligned}\left[\left(\operatorname {grad} f\right)(\Phi (r,\theta ,\zeta ))\right]\cdot \left({{\mathbf {N} }_{r}}(r,\theta ,\zeta )\right)=&\left(\left({\frac {\partial f}{\partial x}}\right)(\Phi (r,\theta ,\zeta )),\left({\frac {\partial f}{\partial y}}\right)(\Phi (r,\theta ,\zeta )),\left({\frac {\partial f}{\partial z}}\right)(\Phi (r,\theta ,\zeta ))\right)\left({\begin{matrix}\cos \theta \\\sin \theta \\0\\\end{matrix}}\right)\\=&\cos \theta \left(\left({\frac {\partial f}{\partial x}}\right)(\Phi (r,\theta ,\zeta ))\right) \sin \theta \left(\left({\frac {\partial f}{\partial y}}\right)(\Phi (r,\theta ,\zeta ))\right)\\=&\cos \theta \left[\cos \theta \left(\left({\frac {\partial (f\circ \Phi )}{\partial r}}\right)(r,\theta ,z)\right)-{\frac {\sin \theta }{r}}\left(\left({\frac {\partial (f\circ \Phi )}{\partial \theta }}\right)(r,\theta ,z)\right)\right]\\& \sin \theta \left[\sin \theta \left(\left({\frac {\partial (f\circ \Phi )}{\partial r}}\right)(r,\theta ,z)\right) {\frac {\cos \theta }{r}}\left(\left({\frac {\partial (f\circ \Phi )}{\partial \theta }}\right)(r,\theta ,z)\right)\right]\\=&\left({\frac {\partial (f\circ \Phi )}{\partial r}}\right)(r,\theta ,z)\end{aligned}}}$　(6-2-2)

であり、同様に、N_θ(r , θ, ζ) , N_ζ(r , θ, ζ) についても、

${\displaystyle \left[\left(\operatorname {grad} f\right)(\Phi (r,\theta ,\zeta ))\right]\cdot \left({{\mathbf {N} }_{\theta }}(r,\theta ,\zeta )\right)={\frac {1}{r}}\left({\frac {\partial (f\circ \Phi )}{\partial \theta }}\right)(r,\theta ,z)}$ (6-2-3)

${\displaystyle \left[\left(\operatorname {grad} f\right)(\Phi (r,\theta ,\zeta ))\right]\cdot \left({{\mathbf {N} }_{\zeta }}(r,\theta ,\zeta )\right)=\left({\frac {\partial (f\circ \Phi )}{\partial \zeta }}\right)(r,\theta ,\zeta )}$ (6-2-3)

が成り立つ。従って「ベクトル場の円柱座標表示」と同様にして、上の等式が示せる。

ラプラシアン

ラプラシアンについても、r ≠ 0 をみたす任意の(r , θ, ζ) に対して以下の等式が成立する。

${\displaystyle \left(\Delta f\right)\left(\Phi (r,\theta ,\zeta )\right)={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r\left({\frac {\partial (f\circ \Phi )}{\partial r}}\right)\right)(r,\theta ,\zeta ) {\frac {1}{{r}^{2}}}\left({\frac {{{\partial }^{2}}(f\circ \Phi )}{\partial {{\theta }^{2}}}}\right)(r,\theta ,\zeta ) \left({\frac {{{\partial }^{2}}(f\circ \Phi )}{\partial {{\xi }^{2}}}}\right)(r,\theta ,\zeta )}$ (6-2-3)

ベクトル場に作用する微分作用素

発散

X を、x -y -z 空間で定義されたベクトル場とするとき、発散 div の円柱座標系表示として以下の等式が成立する。

${\displaystyle (\operatorname {div} X)(\Phi (r,\theta ,\zeta ))={\frac {1}{r}}\left({\frac {\partial (r\cdot {{X}_{r}})}{\partial r}}\right)(r,\theta ,\zeta ) {\frac {1}{r}}\left({\frac {\partial {{X}_{\theta }}}{\partial \theta }}\right)(r,\theta ,\zeta ) \left({\frac {\partial {{X}_{z}}}{\partial z}}\right)(r,\theta ,\zeta )}$

回転

回転 rot の円柱座標系表示については、次の等式が成立する。

${\displaystyle (\operatorname {rot} X)(\Phi (r,\theta ,\zeta ))=\left({{(\operatorname {rot} X)}_{r}}(r,\theta ,z)\right){{\mathbf {N} }_{r}}(r,\theta ,\zeta ) \left({{(\operatorname {rot} X)}_{\theta }}(r,\theta ,z)\right){{\mathbf {N} }_{\theta }}(r,\theta ,\zeta ) \left({{(\operatorname {rot} X)}_{\theta }}(r,\theta ,z)\right){{\mathbf {N} }_{\zeta }}(r,\theta ,\zeta )}$

ただし

${\displaystyle {{(\operatorname {rot} X)}_{r}}(r,\theta ,z)={\frac {1}{r}}\left({\frac {\partial {{X}_{\zeta }}}{\partial r}}\right)(r,\theta ,z)-\left({\frac {\partial {{X}_{\theta }}}{\partial \zeta }}\right)(r,\theta ,z)}$

${\displaystyle {{(\operatorname {rot} X)}_{\theta }}(r,\theta ,z)=\left({\frac {\partial {{X}_{r}}}{\partial \zeta }}\right)(r,\theta ,z)-\left({\frac {\partial {{X}_{\zeta }}}{\partial r}}\right)(r,\theta ,z)}$

${\displaystyle {{(\operatorname {rot} X)}_{\zeta }}(r,\theta ,z)={\frac {1}{r}}\left({\frac {\partial (r{{X}_{r}})}{\partial r}}\right)(r,\theta ,z)-{\frac {1}{r}}\left({\frac {\partial {{X}_{r}}}{\partial \theta }}\right)(r,\theta ,z)}$

である。

曲線・運動

運動

x -y -z 空間における運動を表す曲線

${\displaystyle c(t)=\left({\begin{array}{l}x(t)\\y(t)\\z(t)\\\end{array}}\right)}$ (8-1-1)

が、r -θ-ζ空間に値を取る曲線

${\displaystyle \gamma (t)=\left({\begin{array}{l}r(t)\\\theta (t)\\z(t)\\\end{array}}\right)}$ (8-1-2)

と、円柱座標変換&Phi:を用いて、

${\displaystyle c(t)=\Phi (\gamma (t))}$ (8-1-3)

と表せるとき、γ(t ) を「曲線c (t ) の円柱座標表示」、あるいは「運動c (t ) の円柱座標表示」と呼ぶ。

式(8-1-3)は、

${\displaystyle \left\{{\begin{array}{l}x=r\cos \theta \\y=r\sin \theta \\z=z\\\end{array}}\right.}$ (8-1-4)

の両辺を時刻t に関する関数と考えること、つまり、

${\displaystyle \left\{{\begin{array}{l}x(r(t),\theta (t),z(t))=r(t)\cos \theta (t)\\y(r(t),\theta (t),z(t))=r(t)\sin \theta (t)\\z(r(t),\theta (t),z(t))=z(t)\\\end{array}}\right.}$ (8-1-5)

と考えることと同じである。

速度ベクトル

x -y -z 空間における運動を表す曲線c (t ) の速度ベクトルv(t )：

${\displaystyle v(t)=\left({\frac {dc}{dt}}\right)(t)}$ (8-2-1)

について以下が成立する。

${\displaystyle \left({\begin{array}{l}{v}_{x}(t)\\{v}_{y}(t)\\{v}_{z}(t)\\\end{array}}\right)=\left({\begin{array}{l}(dx/dt)(t)\\(dy/dt)(t)\\(dz/dt)(t)\\\end{array}}\right)=\left({\begin{array}{c}\cos \theta (t)-r(t)\cdot ((d\theta /dt)(t))\cdot \sin \theta (t)\\\sin \theta (t)-r(t)\cdot ((d\theta /dt)(t))\cdot \cos \theta (t)\\(dz/dt)(t)\\\end{array}}\right)}$ (8-2-2)

但しv_x , v_y , v_z は、それぞれv(t ) のx 成分、y 成分、z 成分を意味する。

また、

${\displaystyle \left\{{\begin{array}{l}{v}_{r}(t)=v(t)\cdot {\textbf {N}}_{r}(c(t))\\{v}_{\theta }(t)=v(t)\cdot {\textbf {N}}_{\theta }(c(t))\\{v}_{z}(t)=v(t)\cdot {\textbf {N}}_{z}(c(t))\\\end{array}}\right.}$ (8-2-3)

のように定義すると、

${\displaystyle \mathbf {v} (t)={{v}_{r}}(t){{\mathbf {N} }_{r}}(c(t)) {{v}_{\theta }}(t){{\mathbf {N} }_{\theta }}(c(t)) {{c}_{z}}(t){{\mathbf {N} }_{z}}(t)}$ (8-2-4)

である。また、以下が成立する。

${\displaystyle \left\{{\begin{array}{l}{v}_{r}(t)=(dr/dt)(t)\\{v}_{\theta }(t)=r(t)\cdot ((d\theta /dt)(t))\\{v}_{z}(t)=(dz/dt)(t)\\\end{array}}\right.}$ (8-2-4)

加速度ベクトル

同様に曲線c (t ) の加速度ベクトルa(t ) ：

${\displaystyle {\textbf {a}}(t)=\left({\begin{array}{l}{\frac {d{\textbf {v}}}{dt}}\end{array}}\right)(t)}$ (8-3-1)

については以下が成立する。

${\displaystyle \mathbf {a} (t)={{a}_{r}}(t){{\mathbf {N} }_{r}}(c(t)) {{a}_{\theta }}(t){{\mathbf {N} }_{\theta }}(c(t)) {{a}_{z}}(t){{\mathbf {N} }_{z}}(c(t))}$ (8-3-2)

但しa_x , a_y , a_z は、それぞれ a(t ) のx 成分、y 成分、z 成分を意味する。また、

${\displaystyle \left\{{\begin{array}{l}{a}_{r}(t)=a(t)\cdot {\textbf {N}}_{r}(c(t))\\{a}_{\theta }(t)=a(t)\cdot {\textbf {N}}_{\theta }(c(t))\\{a}_{z}(t)=a(t)\cdot {\textbf {N}}_{z}(c(t))\\\end{array}}\right.}$ (8-3-2)

である。

さらに、以下が成立する。

${\displaystyle \left\{{\begin{array}{l}{{a}_{r}}(t)=[(({{d}^{2}}r/d{{t}^{2}})(t))-{{((d\theta /dt)(t))}^{2}}]\\{{a}_{\theta }}(t)=[2((dr/dt)(t))(((d\theta /dt)(t))) (r(t))(({{d}^{2}}\theta /d{{t}^{2}})(t))]\\{{a}_{z}}(t)=({{d}^{2}}z/d{{t}^{2}})(t)\\\end{array}}\right.}$ (8-3-4)

脚注